Tam Sayılar

BİR DOĞAL SAYININ ÇARPANLARI / BÖLENLERİ

Her doğal sayı iki doğal sayının çarpımı olarak yazılabilir. Bu doğal sayılara o sayının çarpanı denir. Bu çarpanlar aynı zamanda o sayıyı kalansız böldüğü için çarpanlara aynı zamanda bölenidir de diyebiliriz.

ÖRNEK: 24 sayısının çarpanlarını (kalansız bölenlerini) bulalım.

24’ü iki sayının çarpımı şeklinde yazalım. Aşağıdaki gibi sonuçlar elde ederiz.

24 = 1 x 24
24 = 2 x 12
24 = 3 x 8
24 = 4 x 6

Buna göre yukarıda yazdığımız sayılar 24’ün çarpanlarıdır.

24’ün Çarpanları = 1, 2, 3, 4, 6, 8, 12, 24

Bu çarpanlar aynı zamanda 24’ü kalansız böler.

24’ün Kalansız Bölenleri = 1, 2, 3, 4, 6, 8, 12, 24

BİR DOĞAL SAYININ KATLARI

Bir doğal sayının kalansız böldüğü sayıların tümüne o sayının katları denir.

ÖRNEK: 6 sayısının 50’den küçük katlarını bulalım.

6, 12, 18, 24, 30, 36, 42, 48

ÖRNEK: 15 sayısının 50 ile 100 arasındaki katlarını yazalım.

15 x 4 = 60
15 x 5 = 75
15 x 6 = 90

ÖRNEK: 15 sayınının çarpanlarını (kalansız bölenlerini) bulalım.

15 = 1 x 15
15 = 3 x 5

NOT: Bir sayının çarpanları (kalansız bölenleri), o sayının katlarının da çarpanlarıdır yani katlarını da kalansız böler.                                               

KALANSIZ BÖLÜNEBİLME

Bir doğal sayı, bir sayma sayısına bölündüğünde kalan 0 (sıfır) oluyorsa bu işleme kalansız bölme işlemi denir ve “bu doğal sayı, o sayma sayısına tam olarak bölünüyor” veya “bu doğal sayı, o sayma sayısına kalansız bölünebiliyor” denir.

BÖLÜNEBİLME KURALLARI

2 ile Bölünebilme Kuralı

Birler basamağındaki rakam 0,2,4,6,8 olan sayılar 2 ile kalansız bölünebilir. İki ile kalansız bölünebilen sayılara çift sayılar denir. Diğer bir ifade ile birler basamağı 0,2,4,6,8 olan sayılar çift sayılardır.

ÖRNEK: 120, 32, 2018 sayıları çift sayılardır ve 2 ile kalansız bölünebilirler.

SORU: 541A sayısı 2 ile kalansız bölünebiliyorsa A yerine gelebilecek rakamların toplamı kaçtır?

2 ile kalansız bölünüyorsa çift sayıdır ve A = 0, 2, 4, 6, 8 olur. Cevap 0+2+4+6+8=20’dir.

İki ile kalansız bölünemeyen (1 kalanını veren) sayılara tek sayılar denir. Diğer bir ifade ile birler basamağı 1,3,5,7,9 olan sayılar tek sayılardır.

ÖRNEK: 121, 33, 2017 sayıları tek sayılardır ve 2 ile bölündüğünde 1 kalanını verirler.

SORU: 276B sayısı 2’ye tam bölünemiyorsa B yerine gelebilecek rakamların çarpımı kaçtır?

2’ye tam bölünemiyorsa B tek sayıdır ve B = 1, 3, 5, 7, 9 olur. Cevap 1x3x5x7x9=945’tir.

3 ile Bölünebilme Kuralı

Bir doğal sayının basamaklarındaki rakamların sayı değerleri toplamı 3 ile kalansız (tam) bölünüyorsa bu sayı 3 ile kalansız (tam) bölünebilir.

ÖRNEK: 2352 sayısı 3 ile tam bölünebilir.

Çünkü bu sayının rakamları toplamı:

2+3+5+2=12’dir. 12 sayısı 3’ün katı olduğu için 2352 sayısı 3’e kalansız bölünebilir.

ÖRNEK: 2017 sayısı 3 ile tam bölünemez. Çünkü bu sayının rakamları toplamı:

2+0+1+7=10’dur. 10 sayısı 3’ün tam bir katı olmadığı için 2017 sayısı 3’e tam bölünemez, kalanlı bölünebilir.

NOT: Rakamları toplamının 3 ile bölümünden kalanı, sayının 3 ile bölümünden kalanıyla aynıdır.

ÖRNEK: 2017 sayısının 3 ile bölümünden kalanı bulalım.

2+0+1+7=10’dur. 10’un 3 ile bölümünden kalan 1 olduğu için 2017’nin 3 ile bölümünden kalan 1’dir.

SORU: 276A sayısı 3 ile kalansız bölünebiliyorsa A yerine gelebilecek rakamların toplamı kaçtır?

3 ile kalansız bölünüyorsa rakamları toplamı 3’ün katı olmalıdır.

2+7+6+A

15+A sayısı 3’ün katı olmalı.

A yerine 0,3,6,9 yazarsak bu sayının rakamları toplamı 3’ün katı olur.

A yerine yazabileceğimiz rakamların toplamı = 0+3+6+9=18’dir.

6 ile Bölünebilme Kuralı

Bir sayı hem 2 hem de 3 ile kalansız bölünebiliyorsa bu sayı 6 ile kalansız bölünebilir. Yani rakamları toplamı 3’ün katı olan çift sayılar 6’ya tam bölünebilir.

ÖRNEK: 510 sayısı 6 ile kalansız bölünebilir çünkü çift sayı olduğu için 2’ye, rakamları toplamı (5+1+0=6) 3’ün katı olduğu için 3’e tam bölünür.

ÖRNEK: 285 sayısı 6 ile kalansız bölünemez. (Çünkü 3’e tam bölünebilse bile 2’ye tam bölünemiyor.)

ÖRNEK: 724 sayısı 6 ile kalansız bölünemez. (Çünkü 2’ye tam bölünebilse bile 3’e tam bölünemiyor.)

5 ile Bölünebilme Kuralı

Bir doğal sayının birler basamağındaki rakam 0 veya 5 ise bu sayı 5’e kalansız bölünebilir.

ÖRNEK: 2530 sayısı 5’e tam bölünebilir.

Çünkü bu sayının birler basamağı 0’dır.

ÖRNEK: 2014 sayısı 5’e tam bölünemez.

Çünkü bu sayının birler basamağı 4’dır.

NOT: Bir sayının 5 ile bölümünden kalanı, birler basamağındaki rakamın 5 ile bölümünden kalanı ile aynıdır.

ÖRNEK: 2023 sayısının 5 ile bölümünden kalanı bulalım.

2023 sayısı 5’e tam bölünemez. Kalan 3’tür.

ÖRNEK: 569 sayısının 5 ile bölümünden kalanı bulalım.

569 sayısı 5’e tam bölünemez. 9’un 5’e bölümünden kalan 4 olduğu için 569’un 5’e bölümünden kalan 4’tür.

10 ile Bölünebilme Kuralı

Bir doğal sayının birler basamağındaki rakam 0 ise bu sayı 10’a kalansız bölünebilir.

ÖRNEK: 2530 sayısı 10’a tam bölünebilir.

Çünkü bu sayının birler basamağı 0’dır.

ÖRNEK: 2014 sayısı 10’a tam bölünemez.

Çünkü bu sayının birler basamağı 4’dır.

NOT: Bir sayının 10 ile bölümünden kalanı bu sayının birler basamağındaki rakam ile aynıdır.

ÖRNEK: 2023 sayısının 10 ile bölümünden kalan 3’tür.

9 ile Bölünebilme Kuralı

Bir doğal sayının basamaklarındaki rakamların sayı değerleri toplamı 9 ile kalansız (tam) bölünüyorsa bu sayı 9 ile kalansız (tam) bölünebilir.

ÖRNEK: 5436 sayısı 9 ile tam bölünebilir.

Çünkü bu sayının rakamları toplamı:

5+4+3+6=18’dir. 18 sayısı 9’un katı olduğu için 5436 sayısı 9’a kalansız bölünebilir.

ÖRNEK: 2014 sayısı 9 ile tam bölünemez. 

Çünkü bu sayının rakamları toplamı:

2+0+1+4=7’dir. 7 sayısı 9’un tam bir katı olmadığı için 2014 sayısı 9’a tam bölünemez, kalanlı bölünebilir.

NOT: Rakamları toplamının 9 ile bölümünden kalanı, sayının 9 ile bölümünden kalanıyla aynıdır.

ÖRNEK: 5451 sayısının 9 ile bölümünden kalanı bulalım.

5+4+5+1=15’tir. 15’in 9 ile bölümünden kalan 6 olduğu için 5451’ün 9 ile bölümünden kalan 6’dır.

SORU: 735A sayısı 9 ile kalansız bölünebiliyorsa A yerine gelebilecek rakamların toplamı kaçtır?

ÇÖZÜM: 9 ile kalansız bölünüyorsa rakamları toplamı 9’un katı olmalıdır.

7+3+5+A

15+A sayısı 9’un katı olmalı.

A yerine 3 yazarsak bu sayının rakamları toplamı 18 olur ve 9 ile kalansız bölünebilir.

4 ile Bölünebilme Kuralı

Son iki basamağı 00 veya 4’ün katı olan sayılar 4 ile kalansız bölünebilir.

ÖRNEK: 120, 312, 2000 sayıları 4’e tam bölünebilirler.

ÖRNEK: 2345, 142, 215 sayıları 4’e tam bölünemez.

SORU: 871A sayısı 4 ile kalansız bölünebiliyorsa A yerine gelebilecek rakamların toplamı kaçtır?

ÇÖZÜM: 4 ile kalansız bölünüyorsa son iki basamağı:

8712 ve 8716 olabilir. A yerine yazılabilecek rakamların toplamı: 2+6=8’dir.

NOT: Bir sayının 4 ile bölümünden kalanı, son iki basamağındaki rakamların oluşturduğu sayının 4 ile bölümünden kalanı ile aynıdır.

ÖRNEK: 2023 sayısının 4 ile bölümünden kalanı bulalım.

23 sayısının 4’e bölümünden kalan 3 olduğu için 2023 sayısının 4 ile bölümünden kalan 

3’tür.

ASAL SAYILAR

1 ve kendisinden başka hiç bir sayma sayısına tam bölünemeyen 1’den büyük doğal sayılara asal sayı denir. Diğer bir ifade ile çarpanları sadece 1 ve kendisi olan 1’den büyük doğal sayılardır. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 … sayıları birer asal sayıdır.

ÖRNEK: 2, 5, 4, 15 sayılarından hangileri asaldır bulalım.

2 sayısı sadece 1 ve 2’ye kalansız bölünür. Bu yüzden asal sayıdır.
5 sayısı sadece 1 ve 5’e kalansız bölünür. Bu yüzden asal sayıdır.
4 sayısı 1’e, 2’ye ve 4’e kalansız bölünür. Bu yüzden asal sayı değildir.
15 sayısı 1’e, 3’e, 5’e ve 15’e kalansız  bölünür. Bu yüzden asal sayı değildir.

Asal Sayılar ile İlgili Bilgiler

► 1 asal sayı değildir.

► 2 en küçük asal sayıdır.

► 2’den başka çift asal sayı yoktur. (Çünkü hepsi 2’ye de bölünür.)

ASAL ÇARPANLARA AYIRMA

Bir doğal sayıyı asal çarpanlarına ayırmak için iki yöntem kullanabiliriz. Bunlar çarpan ağacı ve bölen listesidir.

1) Çarpan Ağacı

Çarpan ağacı nedir, nasıl yapılır görelim.

Bir sayıyı iki sayının çarpımı şeklinde yazarız (en küçük asal sayıdan başlayabiliriz). Daha sonra bulduğumuz sayıları asal sayı olana kadar bu işleme devam ederiz. Oluşan dalların uçlarındaki sayılar sayımızın asal çarpanlarıdır.

NOT: Çarpan ağacında dalların uçlarındaki asal sayıların çarpımı, çarpanlarına ayırdığımız sayıyı verir.

ÖRNEK: 36 sayısını çarpan ağacı kullanarak asal çarpanlarına ayıralım.

36 sayısının çarpanları : 1, 2, 3, 4, 6, 9, 12, 18, 36’dır. Bunu bir sayının çarpanları konumuzda öğrenmiştik. Bu sayılardan asal sayı olanları asal çarpanlarımızdır.

36 sayısının asal çarpanları: 2 ve 3’tür. Şimdi bunu çarpan ağacı ile bulalım:

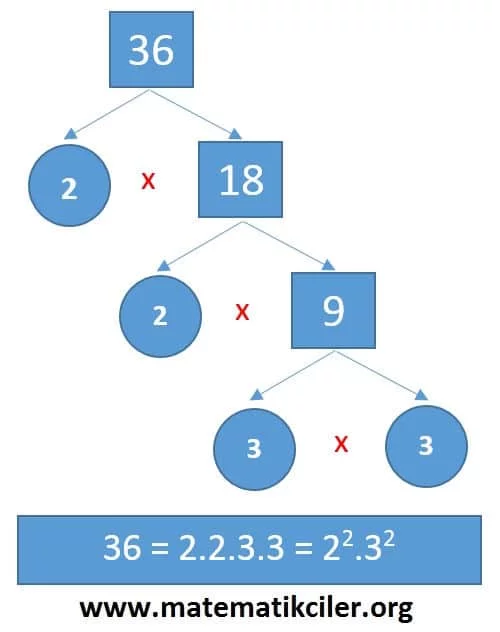
2) Asal Çarpanlar Algoritması (Bölen Listesi)

Asal Çarpanlar Algoritması nedir, nasıl yapılır görelim.Sayımızın yanına dikey bir çizgi çekeriz ve en küçük asal sayıdan başlayarak ve tam bölünmediğinde bir sonraki asal sayıya geçerek bölme işlemi yaparız. 1’i elde edince işlemimiz sona erer. Çizginin sağında kalan sayılar sayımızın asal çarpanlarıdır.

ÖRNEK: 36 sayısını asal çarpanlar algoritması ile asal çarpanlarına ayıralım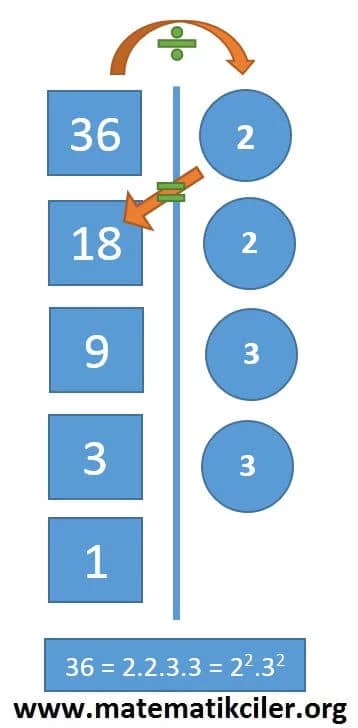

NOT: Bölen listesinde çizginin sağındaki asal sayıların çarpımı, çarpanlarına ayırdığımız sayıyı verir.

DOĞAL SAYILARIN ORTAK KATLARI

İki ya da daha fazla doğal sayının katları arasından ortak olanlarına, bu sayıların ortak katları denir.

ÖRNEK: 6 ve 4 sayılarının ortak katlarını bulalım.► Öncelikle 6 ve 4 sayılarının katlarını ayrı ayrı yazalım:

6’nın katları : 6, 12, 18, 24, 30, 36, 42, 48, …

4’ün katları : 4, 8, 12, 16, 20, 24, 28, 32, 36, …

► Şimdi bu katlardan ortak olanlarını işaretleyelim.

6’nın katları : 6, 12, 18, 24, 30, 36, 42, 48, …

4’ün katları : 4, 8, 12, 16, 20, 24, 28, 32, 36, …

4 ve 6’nın ortak katları: 12, 24, 36, 48, ….

İki ya da daha fazla doğal sayının ortak katları, bu sayıların ilk (en küçük) ortak katının katlarından oluşur. Örneğin yukarıdaki örnekte 4 ve 6’nın ortak katları (12, 24, 36, 48, …), bu sayıların en küçük ortak katı olan 12’nin katlarıdır.

DOĞAL SAYILARIN ORTAK BÖLENLERİ

İki ya da daha fazla doğal sayıyı aynı anda bölen sayılara, bu sayıların ortak böleni denir.

ÖRNEK: 36 ve 24 sayılarının ortak bölenlerini bulalım.

► Öncelikle 36 ve 24 sayılarının bölenlerini ayrı ayrı yazalım:

36’nın bölenleri : 1, 2, 3, 4, 6, 9, 12, 18, 36

24’ün bölenleri : 1, 2, 3, 4, 6, 8, 12, 24

► Şimdi bu bölenlerden ortak olanlarını işaretleyelim.

36’nın bölenleri : 1, 2, 3, 4, 6, 9, 12, 18, 3624’ün bölenleri : 1, 2, 3, 4, 6, 8, 12, 24.

36 ve 24’ün ortak bölenleri: 1, 2, 3, 4, 6, 12’dir.

İki ya da daha fazla doğal sayının ortak bölenleri, bu sayıların en büyük ortak böleninin bölenlerinden oluşur. Örneğin yukarıdaki örnekte 32 ve 24’ün ortak bölenleri (1, 2, 3, 4, 6, 12), bu sayıların en büyük ortak böleni olan 12’nin bölenleridir.

Çarpanlar ve Katlar Formunu Dolduralım :

https://docs.google.com/forms/d/e/1FAIpQLScOEnW8X05mDX-yppxFp23oElRsV4X7L83-Ro34bYn5c4sfzw/viewform?usp=header                                                                                                                

Quiz Yapalım :

https://quizizz.com/embed/quiz/67924be5a3fce4d97edf1ba9.     

Test Çözelim :

https://create.kahoot.it/share/6-snf-carpanlar-ve-katlar/b6f7ae0f-7405-465f-a1d6-f0c1268920cc.  

Oyun Oynayalım : 

<iframe style="max-width:100%" src="https://wordwall.net/tr/embed/942d1d8458a44440a7efedaf4b66ede0?themeId=1&templateId=3&fontStackId=0" width="500" height="380" frameborder="0" allowfullscreen></iframe>   

Video İzleyelim : https://youtu.be/NfPw-PRedKU?si=g8POTAQvAMHorqMX   

Kavram Haritamızı İnceleyelim:https://atlas.mindmup.com/2025/01/7dd6c150d99711ef8502a7da2b4b2df4/_arpanlar_ve_katlar/index.html